Python学習【365日チャレンジ!】231日目のマスターU(@Udemy11)です。
眠たすぎて頭がカックンカックンしながら、コードを打っていたら、dが永遠続いて入力されていることに気がついて、めっちゃビビりました。
こんな経験ありませんか?
アフィリエイターの方なら、たくさん記事を書かないと成果は上がらないので、こんな経験されたことがあると思うのですが、普通に働いている方ならあまりこんな経験はないのかもしれません。
もしかしたらプログラマーの方にとっては、気づけばわけのわからない文字列が記述されていたなんてことは日常茶飯事かもしれませんね。
睡魔には勝てないので、しっかりと睡眠をとって学習をすすめるようにしましょう。
それでは、今日もPython学習をはじめましょう。
昨日の復習
昨日は、プロセスの並列処理を簡単にできるProcessPoolExecutorについて学習しました。
ThreadPoolExecutorと同じコードでProcessPoolExecutorに変更するだけでスレッドからプロセスの並列処理に変更することができました。
詳細については、昨日の記事をごらんください。
昨日で並列化のセクションが終了したので、次のセクションである暗号化に進みますが、その前にプログラミングには必要不可欠な2進数、10進数、16進数について学習したいと思います。
パソコンが計算に使っているのは、0と1のデータだけの2進数であるということは知っていたのですが、いまいちきちんと理解できていませんでした。
16進数なんてことになると、全くもってなんのことやらさっぱりわかっていませんでした。
私が理解できていたのは、10進数だけなのですが、どうやらプログラミングの世界では、この2進数と16進数が必要になるらしいので、基礎から勉強したいと思います。
進数とは
まず、進数(base number)というのは、進数の前に記載されている数字の数より多くなった時に桁が1つ繰り上がる計算方法です。
人間の指は、10本なので、10進数が理解しやすく、コンピューターはオンとオフという2つの情報だけがある2進数が理解しやすいから、それぞれ10進数と2進数が使われています。
すべて0から始まり、10進数は10個目の次、つまり11個目の値(10)で桁が一つ繰り上がり、2進数は、2個目の次、つまり3個目の値(2)で桁が一つ繰り上がります。
なので、16進数は、16個目の次、17個目の値(16)で桁が一つ繰り上がる計算方法です。
10進数
10進数は私たち人間に最も理解しやすい計算方法ですが、一般的には1から10までと考えますが、0から9までの数字を使います。
どの進数も1つ目の値は0なので、ちょっと引っかかるかもしれませんが、これまで学習してきたPythonの関数のインデックスなども0から始まっていたので、ここまで学習してきた人にとってはスムーズに理解できると思います。
ま〜、10進数でつまづく人はあまりいないと思いますが、重要なポイントを抑えておく必要があります。
10進数の1056は、
10の3乗×1 + 10の2乗×0 + 10の1乗×5 + 10の0乗×6
ということです。(ちなみに10の0乗は1です)
この考え方は、2進数と16進数でも同様で、10進数との変換に役立ちますので、気にかけておきましょう。
2進数
2進数は、0と1だけを使っているので、3つ目の値で桁が一つ繰り上がります。
つまり、0→1→10となるわけです。
10進数と2進数の値を並べてみました。
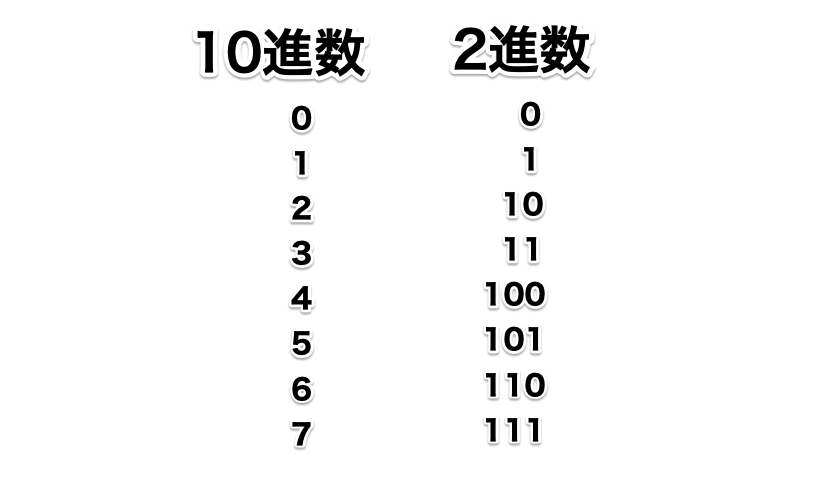
0と1は同じで、10進数の2が2進数では桁が上がって10(イチゼロ)になります。
ちなみに、2進数には、0(ゼロ)と1(イチ)しかないので、10はイチゼロで、100はイチゼロゼロと読みます。
10進数の考え方同様に、2進数の1101を表示してみます。
2の3乗×1 + 2の2乗×1 + 2の1乗×0 + 2の0乗×1
となりますが、2以上の値は2進数にはありませんので、この計算で2進数を10進数に変換することができます。
8×1 + 4×1 + 2×0 + 1×1 =
13
2進数の1101は、10進数の13になるということです。
16進数
16進数は、1桁に16個の値があり、0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,Fの値を使います。
17個目の値は桁が一つ繰り上がり、10(イチゼロ)になります。
10進数と16進数と2進数を並べてみました。
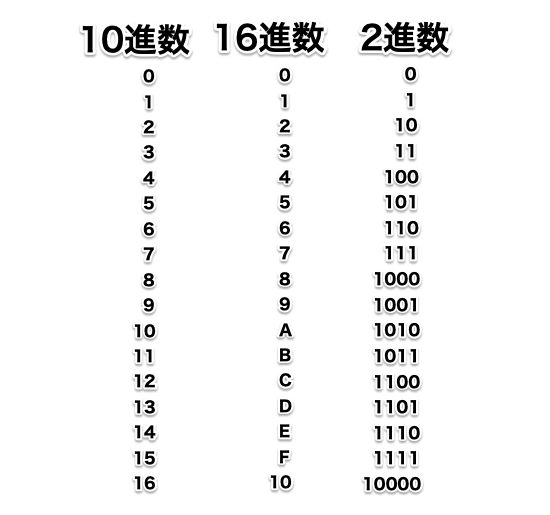
1桁に16個の値があるのが16進数です。
2進数同様に、例題として16進数の10A3を10進数に変換してみましょう。
16の3乗×1 + 16の2乗×0 + 16の1乗×A(10) + 16の0乗×3
となりますので、10進数への変換の計算をしてみます。
4096×1 + 256×0 + 16×10 + 1×3 =
4259
これで2進数から10進数、16進数から10進数への変換が理解できたかと思うので、次は反対の変換を考えてみましょう
10進数から2進数へ
10進数から2進数へ変換するには、10進数の数を2で割って余りの数を求めます。
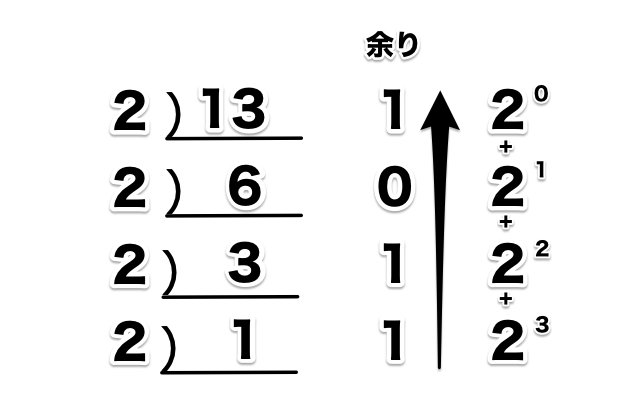
10進数の13を2で割っていき余りを求めて反対から並べると2進数になるので、結果は1101になります。
10進数から16進数へ
同じように、10進数を16進数へ変換するには、10進数の数を16で割って余りの数を求めます。
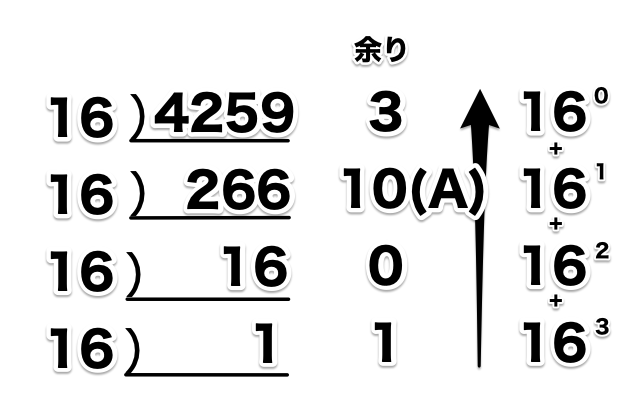
10進数の4259を16で割っていき、反対から並べれば、16進数になります。
ちなみに、余り10は16進数のAとなるように、B(11),C(12),D(13),E(14),F(15)への変換は必要になります。
結果は10A3です。
ちょっと理解するのに時間がかかるかもしれませんが、10進数でも同じように考えるとわかりやすいかもしれません。
1024を10で割っていくと。。。
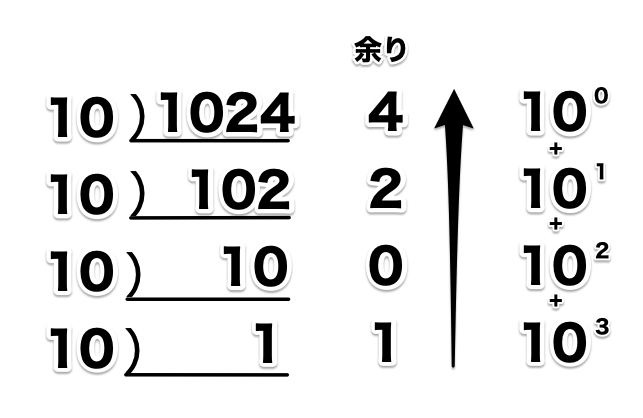
当たり前のことなんだけど、こうやって考えると2進数だろうが16進数だろうが、7進数だろうが理解することができるようになります。
2進数と16進数の変換
2進数と16進数の変換は少し特殊です。
16は2の4乗なので、2進数の4桁が16進数の1桁になります。
例えば2進数の10001111は、8桁ですが、16進数にすると2桁になるので、2進数を1000と11114桁づつに分けて考えます。
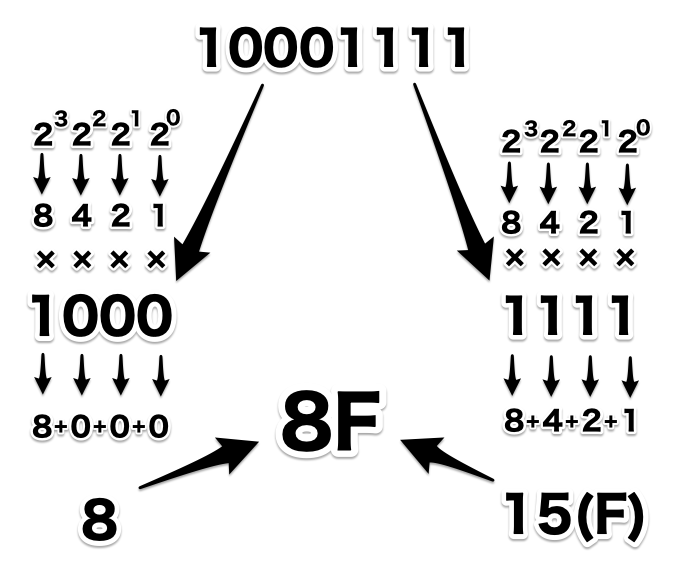
2進数を4桁づつに分けて、2の3乗の桁、2乗の桁、1乗の桁、0乗の桁の値をそれぞれ掛け合わせて10進数にします。
その後、10進数の10〜15の値を16進数のA〜Fの値に変換して、くっつければ2進数から16進数への変換ができます。
16進数から2進数への変換はこの逆で、16進数を1桁づつ10進数に変換して、2の3乗つまり8以上なら2進数の4桁の一番左を1にして値から8を引く、次は2の2乗(4)以上なら3桁目を1にして4を引く、次は2の1乗(2)以上なら2桁目を1にして2を引く、最後は1か0なので、その値を1桁目に入れれば完成です。
ちなみに4桁目、3桁目の条件に合わない場合は1ではなく、0を入れて次の桁に移ります。
例えば16進数の71を考えてみると、まずは7と1に分けて、7から考えます。
8未満なので、4桁目は0、3桁目は4以上なので、1として、3が残ります。
2桁目は2以上なので1にして1が残り、1桁目はそのまま1になり、左の4桁は最初の0がいらないので、111になります。
同じように残りの1を考えてみると、8未満、4未満、2未満なので、結果は0001で、こちらは大きい桁(左側)が存在しているので、0を省略することはできません。
合わせると、1110001になるわけですね。
ちょっとしたコツ
今回の学習に関して、参考にさせてもらったのが、以下の記事になります。
ちょっとしたきっかけで今まで理解できていなかったことが理解できたりするので、ぜひこの機会に2進数と16進数について理解を深めてください。
少しPythonから離れたような感じの学習でしたが、プログラミングを学習するために理解しておくべき前提条件でもあるので、しっかり理解しておきましょう!
それでは明日もGood Python!